Sunday, October 30, 2005
Liverpool 2-0 West Ham
Garcia and Morientes looked good, and Zenden scored his first goal. Given how little he had to do, Reina had the odd shaky moment, but overall I have to be pleased. We were very dominant and only some good goalkeeping and a double clearance off the line kept the score down.
Saturday, October 29, 2005
May's Theorem
a) Proof of May’s Theorem[1]
May gives four necessary and sufficient conditions for simple majority rule[2]:
Decisiveness: “the method must be decisive and universally applicable, or more briefly always decisive, since it must specify a unique decision (even if this decision is to be indifferent) for any individual preferences.” (p.681)
Anonymity: “The group decision function is a symmetric function of its arguments… D is determined only by the values of the Di that appear, regardless of how they are assigned to individuals as indicated by subscripts (names). A more usual name is equality.” (p.681)
Neutrality: “the method of group decision does not favor either alternative. A precise way of stating this is that if the names of x and y are reversed, the result is not changed.” (p.681)
Positive responsiveness: “if the group decision is indifference or favourable to x, and if the individual preferences remain the same except that a single individual changes in a way favourable to x, then the group decision becomes favourable to x.” (p.682)
May states these conditions are necessary for majority-rule – nothing is majority rule unless it satisfies them. Secondly he states they are sufficient, anything satisfying them is majority-rule.
That majority-rule decision function (D) can be represented as sum of N(1), N(0) and N(-1); where N(1) is the number of votes for x and N(-1) as votes for y. Those who are indifferent, N(0), don’t matter here. If D=0 the social decision is indifference. If D>0 the social decision =+1, and if D<0 it is –1.
That majority rule therefore satisfies the four conditions is fairly obvious. It always produces an outcome of +1, 0 or –1. This is true even when individual inputs (votes) change. Swapping a +1 and a –1 ballot doesn’t affect the result, the sum is unchanged. The same voting patterns on another issue (e.g. a against b) would produce the same sum, and thus the same result – there is no bias to the status quo, as there would be if, e.g. a two-thirds majority were required. Finally an increase in any Di will increase the sum D, and thus ensure positive responsiveness, e.g. if D was non-negative it would become positive.
Next we have to show any procedure satisfying the four conditions is majority-rule, i.e. that they are sufficient for majority-rule. If N(-1) = N(1), i.e. votes are tied, it follows from the first three conditions that the social decision is indecisive, i.e. D=0. If x were to win, i.e. D=1, then swapping all +1s and –1s would either produce the reverse result, so anonymity would be violated, or the same result in which case neutrality would be violated. Further, if N(1) = N+1(-1), i.e. one y-voter becomes indifferent and abstains, so there is one more x-voter than y-voter, then the social decision must prefer x, from positive responsiveness. Thus the four conditions imply simple majority-rule.
b) Evaluation of May’s Theorem
May’s theorem merely defines necessary and sufficient conditions for simple majority-rule. It is not clear that his conditions are always desirable, as is the case with Arrow’s.
Decisiveness I take to be relatively uncontroversial. We want a procedure that always yields outcomes, even if those outcomes are to be indifferent. After all, if politics is supposed to be war by other means[3], we need a political solution – otherwise we may end up resorting again to violence.
Anonymity, as May points out, is basically equality between voters. This seems obviously desirable. Even if we wanted some voters to count for more[4], in order to correctly weight their number of votes, we would want each vote to count equally, and thus be anonymous.
Neutrality is the condition that no option is favoured. This rules out requiring super-majorities, or a bias in favour of the status quo. This may be generally desirable, but it is not always so – often constitutions are ‘entrenched’ so that they require, e.g. a two-thirds majority to amend. May has nothing to say about this, other than that such is obviously not simple majority-rule. For ordinary political decisions, however, it seems neutrality is preferable. A bias in favour of the status quo would effectively mean those voting for it (though unidentified a priori) would count for more than those voting against it.
It is the final one of May’s conditions that I find most problematic. Positive responsiveness, as he defines it, is quite stringent – much more so than Arrow’s positive monotonicity or non-negative responsiveness[5]. May requires that where there is indifference, a single voter can become decisive. I am not sure I share this intuition. Suppose there are millions of voters involved – many of whom are indifferent, but those for x exactly balance those for y. What May’s condition means is that if just one of the indifferent voters decides to vote for x, then x is now an outright winner. It’s not clear to me that a conflict between 1,000 and 1,001 should be decided simply by reference to the numbers[6]. Just because the other members of society ‘balance out’ it is not obvious that one other should be able to determine the social decision[7].
Lottery-voting is decisive (the vote picked determines the outcome), anonymous (all votes have an equal chance of being picked) and neutral (no outcome is particularly favoured – the chances of each outcome depend only on the number of votes it gets). It is May’s positive responsiveness that lottery-voting ‘fails’, but this simply tells us that lottery-voting is not simple majority-rule (because satisfying these four conditions is sufficient for being such, anything that isn’t majority-rule must fail one). As I have said, however, this demand does not seem normatively compelling to me. Lottery-voting satisfies Arrow’s weaker axiom – a vote for x always increases x’s chances of victory[8].
Another advantage of lottery-voting is that it is easily applicable to cases with more than two options. May is working in a context where voters choose simply between x and y (as in a two party election). It is this context that necessarily means indifferent voters are ignored. For May, if there are two votes for x and three for y, then y is ‘socially preferred’ even if a million people are indifferent. Voters who want the social outcome to be indifference can only attempt to bring this about by voting for whichever option they think is in the minority, and even then it is a fine balancing acting, as only an exactly equal balance results in social indifference – indifference can’t be registered as a ‘positive preference’, as this would be to introduce a third option.
That May is only working in a two-option framework isn’t itself a criticism, but it shows the limits of his theorem, as politics almost always involves more than two options – and while a larger number may be artificially reduced to two (e.g. by AV or STV) there is no fair way of doing this[9], and the voting system is no longer simple majority-rule as in any case it has to eliminate the other options first. Lottery-voting can be straightforwardly applied to cases with more than two options, and still respects decisiveness, anonymity, neutrality and non-negative responsiveness.
[1] Following D. C. Mueller (2003) Public Choice III pp.135-6.
[2] K. O. May (1952) ‘A Set of Independent Necessary and Sufficient Conditions for Simple Majority Decision’ Econometrica 20:4 680-684 (references in parentheses refer to this article).
[3] I reverse Clausewitz’ aphorism. War I assume came first, before politics emerged as a peaceful way of resolving conflicts. C.f. A. Przeworski ‘Minimalist Conception of Democracy: A Defense’ in I. Shapiro and C. Hacker-Cordan (eds.) (1999) Democracy’s Value p.48. It’s possible that majority rule developed from counting the numbers on each side and giving victory to the greater number on the basis they were most likely to win a violent contest. This would also explain why the franchise was originally linked to fighting ability – i.e. restricted to men, and particularly the rich (hoplite class).
[4] See, e.g., Aristotle, Fleurbaey. C.f. Banzhaf on weighted voting.
[5] See May p.682, fn.8.
[6] In another context, I seem to be joined by Frances Kamm – who describes an extra person in this case as an ‘irrelevant’ utility’ – John Broome and Iwao Hirose.
[7] Note this is not the same as the median voter theorem, in which the one in the middle gets their way because others are balanced on either side – because (as will be highlighted later) the median is a placeholder for whoever happens to be in the middle – there is not one decisive voter who can throw the decision either way.
[8] A condition that rules out STV.
[9] Riker (1982) Liberalism Against Populism: A confrontation between the theory of democracy and the theory of social choice pp.59-60.
Median Voter Theorem
c) Proof of Median Voter Theorem
The median voter theorem state that if voters’ “curves are singled-peaked, Omed. will be able to get a simple majority over any of the other motions a1,…, am put forward”[1]. This is quite straightforward, at least if n (number of voters) is odd[2]. Any proposed solution to the right of the median voter’s ideal will be able to gain the support of all voters to its right, and those between the proposal and the median who are ideologically closer to the proposal (for whom the proposal represents something slightly too far right, as opposed to quite a bit too far left). Opposition, on the other hand, will include the median voter himself and all to the left – amounting to [(n-1)/2]+1, i.e. a majority. Similarly there will be a majority of the median voter and all to his right that would defeat any move to the left.
The original theorem assumed a single left-right spectrum in one-dimensional issue space. In fact, it can be extended to multidimensional space[3], if the ‘median’ voter has the others in opposing pairs around him. For example, imagine a cross-shape with the median voter at the intersection of the two lines, and four others at compass points (N, S, E, W). The status quo is the median voter’s ideal. A move to the NW, for example, will be opposed by three – the median voter and those at S and E. (Note though, a move directly to N will get one for, two against [median and S] and two indifferent [W and E] – it’s possible if N could offer the latter two some small incentive that they might vote for such a move).
d) Evaluation of Median Voter Theorem
The median voter theorem explains why in two party systems we end up with two parties with very similar platforms. Those on the ideological extremes are assumed their safe, core voters. It is those in the middle of the spectrum that make the difference between 40% and 60% support – and most crucially, the median voter that tips the balance from (say) 49.5% to 50.5%.
The median voter theorem introduces some predictability into political outcomes. It does not mean that the median voter is an Arrovian dictator, however. There is no one individual who will get his way however others vote[4]. Indeed, who is ‘the median’ depends on the voting pattern. One reason why economic redistribution in democracies has perhaps been less than those fearful of extending the franchise expected in the 19th century is that, while the median member of society may have a below (mean) average income, because the poorer generally seem less likely to vote, the median voter may have an above-average income.
Another consequence of the median winning position is that no one is too far away from the outcome, and this limits dissatisfaction – as opposed to someone on the far right winning, leaving the left very dissatisfied. It does not minimise aggregate dissatisfaction (the sum of the differences between each individual and the outcome) though, because those to the left of the median could be much more extreme left wing than those to the right, and thus aggregate dissatisfaction would be reduced if the outcome was moved to the left. Further what may matter on a divisive issue like abortion might be which side of the spectrum one is on, more than how far. If the median voter is pro-life, it wouldn’t matter much to pro-choices that they were only a moderate pro-lifer – still the other side would have won[5].
In any case, the model is not always applicable. Even on a single dimension, voters’ preferences need not be single-peaked. During the Vietnam War, for example, many Americans apparently favoured either a complete withdrawal of troops or sending more in – do it properly or not at all. In such a case, the middle ground need not be stable, as it could be defeated by a proposal at either extreme. When it comes to multidimensional matters, while a median voter can exist, there may not be a unique equilibrium.
Real world politics doesn’t always fit economic models/predictions perfectly. It’s quite possible for parties to drift from the median – e.g. the ‘loony left’ dominated Labour in 1983, though out of touch with the public. At the same time, the Conservatives were further to the right – but Thatcherite policies encouraging house and share ownership effectively helped move the median voter to the right. To regain power, New Labour have moved to the right in pursuit of this median. However, if a party strays too far from its core supporters, new parties may arise on the fringes of the political spectrum – even if they have no hope of winning, the can act as pressure groups – e.g. communists keep socialists ‘honest’ to left-wing ideals.
[1] D. Black (1998) The Theory of Committees and Elections (McLean et al eds.) p.23.
[2] If n is even, the median lies between two voters.
[3] D. C. Mueller (2003) Public Choice III pp.92-3. C.f. C. Plott (1967) ‘A Notion of Equilibrium and Its Possibility under Majority Rule’ American Economic Review 57 787-806.
[4] ‘The median’ is a placeholder, like Rawls’ ‘worst off group’.
[5] Of course, compromises are possible on almost all political decisions. Even on abortion, compromises might involve state funding, maximum time allowed after conception and the stringency of medical reasons required.
Wednesday, October 26, 2005
Football Injuries
Chelsea's Glen Johnson has broken his wrist after punching a wall at his home, according to newspaper reports. He has played only one game for Jose Mourinho's side this season and now faces a lay-off of at least two months.
The Truth of Blogging
enlightened me to the whole point of blogging:
People who are trying to decide whether to create a blog or not go through a
thought process much like this:
1. The world sure needs more of ME.
2. Maybe I’ll shout more often so that people nearby can experience the joy of knowing my thoughts.
3. No, wait, shouting looks too crazy.
4. I know – I’ll write down my daily thoughts and badger people to read them.
5. If only there was a description for this process that doesn’t involve the words egomaniac or unnecessary.
6. What? It’s called a blog? I’m there!
The blogger’s philosophy goes something like this: Everything that I think about is more fascinating than the crap in your head.The beauty of blogging, as compared to writing a book, is that no editor will be interfering with my random spelling and grammar, my complete disregard for the facts, and my wandering sentences that seem to go on and on and never end so that you feel like you need to take a breath and clear your head before you can even consider making it to the end of the sentence that probably didn’t need to be written anyhoo.
Needless to say, the new Dilbert blog - complete with bullet-firing donuts - will one I'm reading regularly...
Several Quick Things
1. Yesterday I went out for dinner with the speaker following the regular Moral Philosophy Seminar. I’d never done that before, but it was quite nice – even if it was a bit expensive at £15 despite being subsidised (I think they picked a wine a bit out of my range to be honest…)
2. This was in spite of having an essay to mark last night. I had (taught) my first tutorial today. I think it went fairly well – at least I was able to get over how strange it felt to be on the other side, and able to raise questions for the student rather than showing up my lack of knowledge. I do worry it may have been more of a Socratic-style ‘aporetic’ experience for her. I hope she learned from being required to think, rather than just getting confused...
3. I went out to the IMSoc (Indie Music Society) event Vertigo at the Cellar. Saw three bands play, of which The Half Rabbits were best – if rather too much like Interpol. The DJs were pretty good too, but the place was absolutely packed.
4. Crystal Palace 2-1 Liverpool. Typical – another case of chances created, us only playing for the first half, and heroic goal-keeping. I honestly would’ve liked to have seen a lot more youngsters used, like last year – it couldn’t have been a worse result after all… Still, we did see Kewell and Gerrard coming back from injury, and at the end of the day the Carling Cup was the least important of this year’s four or five competitions. Last year we crashed out at the first hurdle (Burnley) in the FA Cup remember, so let’s hope we can do better there this time.
Tuesday, October 25, 2005
Who's an Anarchist?
I can't go into the details of the whole paper, but for what it's worth without here's my response:
Do you think, for Ward, there could ever be too much anarchism in an actual society? If he is indeed role-playing, then it suggests he's arguing for anarchism, because we're too far the other side. This is like Aristotle's advice that if our nature tends towards one side of a mean - say, we're moreprone to cowardice than recklessness as a deviation from courage - then we should err on the side of caution, that is be too brave to compensate.
If this is his approach, it suggests that were society to change quiteradically in an anarchist direction, then a role-player might have to switchsides to maintain/restore balance. This, I think, open up a distinction between contingent anarchists' - those who argue for anarchism because they think that here and now we need more anarchy - and those whose ideal is total anarchy, and will argue for it no matter what condition we're in (short of realising it) I thought that might be helpful for your 'what is an anarchist?' question.
I also wondered why you thought to phrase that in necessary and sufficient terms. I don't know if you're familiar with Wittgenstein's 'language games', but he suggests not all concepts are analysable in such terms. The things we call 'games', for example - football, Cludeo, snap, Jenga, etc - don't seem to share necessary/sufficient properties. Wittgenstein's answer was that these concepts don't pick out 'natural kinds', rather we impose them on the world. We learn certain examples, and then choose to extend the term 'game' (or whatever) to new cases we think are sufficiently similar in various aspects. He called these similarities 'family resemblances' (think how members of a family may have overlapping similarities - e.g. a family nose, hair colour, etc - without there being a set of necessary/sufficient characteristics common to all family members)
Since 'anarchism' seems to pick out a family of related views, it seems plausible that something like this holds. There's no 'truth' of the matter towhether a view really is anarchist, it's up to us how far we extend the term. Moreover, we can't give a definite necessary/sufficient checklist of what it takes to be an anarchist. We know certain examples from experience, and when we come to a new borderline case we have to make a judgement about whether or not it is similar enough to other anarchist views to share the name.
Sunday, October 23, 2005
Silly Costumes (an Oxford thing)
Unfortunately, I don't have pics going back to my matriculation, but I do of graduation (17/07/04):
Edit: I found matriculation pictures from this year on the blog of another recent starter in the Politics Department here. Amazing how many Oxford Politics grads are blogging...
Fulham 1-0 Liverpool
Ok, that it went from 1-0 to 2-0 in the 92nd minute doesn’t really bother me – in the circumstances I’d have liked us to press forward. The fact we again couldn’t score – though partly due, ironically, to former Liverpool reserve ‘keeper Tony Warner – is worrying though.
The return of Harry Kewell was great news. The decision to replace our most natural winger – whose crosses Peter Crouch is supposedly to thrive on – with the man who should be on the end of them (Crouch) was, however, utterly baffling. Sure Kewell was unlikely to last 90 minutes, but it would’ve been nice to see him get some chance to link with Crouch.
Replacing Traore with Garcia was also a strange choice. It was Josemi who’d been leaving gaping holes in our backline, so I think the natural course of action would’ve been to replace him – moving Carra to right back and playing Hyypia and Traore central with Riise on the left. Admittedly I’m reluctant to lose Carra from the centre, but the fact is Hyypia and Traore weren’t greatly troubled, and missing both Finnan and Barragan we don’t have many more options at RB. Josemi really has to improve, or go...
So, to sum up, good points:
Return of Harry Kewell
Bad:
Not scoring
Three points dropped
Puzzling substitutions
Josemi
I won’t deny it was disappointing, but up until today I don’t think we’d had that bad a start to the season, and fingers crossed one more win should see us qualify to the Champions League knockout stage.
Saturday, October 22, 2005
Condorcet and Borda Voting Methods
Although the modern ‘social choice’ literature began with Duncan Black in the 1940-50s, major discoveries were originally made – and lost – much earlier, for example by Charles Dodgson (Lewis Carroll) and, most significantly for present purposes, by Borda and Condorcet in the late 18th century (1770-80s). Borda and Condorcet proposed two voting rules now generally known after them, though in fact both may have been anticipated before (even if they were unaware of the fact).
Ramon Lull in his novel Blanquerna (1282-7) proposes a procedure to select two candidates from a larger group. A cell has to be drawn featuring the possible combinations, as illustrated:

Assuming there is no positional element (1st and 2nd) there are 21 possible combinations for choosing two from seven, e.g. A and B (which is equivalent to B and A). Cells marked X are ineligible for votes, as A can’t be compared with him/her-self. The other cells can be used to compare each possible pair, e.g. A against B, A against C, … B against C, etc. The result is a comprehensive pairwise comparison, and Lull’s conclusion is that “the candidate to be elected should be the one with the most votes in the most compartments [cells]”[1]. Unfortunately, ‘the most votes in the most compartments’ is ambiguous. It could mean either each candidate’s total votes (from all cells) are added up, in which case the procedure is equivalent to the Borda count. Alternatively one could simply focus on who wins the most majorities from pairwise comparison – i.e. the Copeland rule, a natural extension of the Condorcet procedure (to which I’ll return later). Despite Borda citing Lull in support of his method, it isn’t actually clear which of these interpretations is correct – nor does it matter greatly to our present attempt to adjudicate between the two.
Borda proposed a rank-order count in 1770. According to this procedure, each elector orders all the n options. First preference is given n-1 points, second preference n-2 and so on down to last (least preferred), which gets no points. The winner is the option with most points. Condorcet proposed a system somewhat like Lull’s, where each option is compared to every other in pairs. A ‘Condorcet winner’ is one that beats every other. There need not be a Condorcet winner, however, as illustrated by the possibility of cycles (a>b, b>c and c>a). In this case, the obvious generalisation is to go with the option that beats more others than any other[2].
It is worth noting at this stage that Condorcet’s procedure needn’t produce the most likely right answer, in spite of his well-known work on juries and probability. Suppose we have the following scenario:
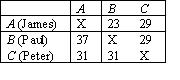
The number of votes for each option is in the appropriate row, with the columns indicating who they are paired against – thus we see B beats A 37 to 23. Note that in this case, C is a Condorcet winner, (narrowly) beating each of the other options 31 to 29.
If v (verité, the probability of an individual’s judgement being correct) is not much more than 0.5 then “the Borda rule is more likely to select the correct winner than is a search for the Condorcet winner, because Paul’s total score counts for more than Peter’s precarious and unreliable majority over him”[3]; i.e, because v is low and so is the winning majority, we cannot be very confident that C (Peter) really is better than B (Paul), or for that matter A (James). The 37 to 23 majority B (Paul) has over A (James), however, means – even with low v – we can be confident that B (Paul) is better than A (James). Whether he fully appreciated that his own logic should drive him to this result, Condorcet was firmly and explicitly against it – perhaps simply due to his personal hostility against Borda. Condorcet insisted we should eliminate A (James) for losing both comparisons, and that it would then be perverse to choose B (Paul) over C (Peter) when a majority prefer C (Peter). Against any alternative (Borda-inspired) method he wrote “The points method confuses votes comparing Peter and Paul with those comparing either Peter or Paul to James. As long as it relies on irrelevant factors to form its judgments, it is bound to lead to error”[4]. The last sentence makes somewhat explicit the principle to which he is appealing, independence of irrelevant alternatives – i.e. the choice between A and B should depend only on the relative merits of those two, not on C[5].
The inspiration behind both methods is to consider more than just first preferences, by looking at how voters rank other options. Thus they go some way towards reducing problems of intense minorities or majority tyranny, by producing a compromise that aims to be somewhat acceptable to all. We can remind ourselves what is at stake by re-producing the following table[6] (from last week), where both rules differ from each other and other common procedures (e.g. plurality, AV).
I (18 people): A D E _ C B
II (12): B E D _ C A
III (10): C B E D _ A
IV (9): D C E _ B A
V (4): E B D _ C A
VI (2): E C D _ B A
Six procedures give different results (I’ve highlighted the two most relevant to us):
1. Simple plurality: A
A wins, with 18 votes (options B-E scoring 12, 10, 9 and 6 respectively).
2. Plurality runoff (AV): B
B beats A in the second round, 37 votes (12+10+9+4+2) to 18.
3. Sequential runoff (STV): C
E, D, and B are eliminated. C wins the final vote, 37 to A’s 18.
4. Borda count: D
As above, each gets four points per first-preference, three points per second-preference… to zero points for a fifth (last) preference. D wins with 136 points = (18x3)+(12x2)+(10x1)+(9x4)+(4x2)+(2x2). A gets 72, B 101, C 107 and E 134.
5. Condorcet: E
The ‘Condorcet winner’ beats each of the other four options in pairwise comparison. Here E wins. E beats A 37-to-18, B 33-to-22, C 36-to-19, and D 28-to-27.
6. Approval voting: D and E tie
Everyone casts a vote for each option they consider ‘acceptable’ – here above the empty cell. A is approved by 18, B by 26, C by 21, and D and E by all 55. Thus D and E tie.
The Borda criterion attempts to most please everyone (collectively), rather than fully-pleasing most (as a simple plurality/majority system). Respecting everyone’s preferences would seem to promote utilitarian outcomes. It would elect someone who was widely popular, even if second choice, over someone who had a narrow majority of first preferences but was otherwise widely detested. For example:
51%: A, B, C,... Y, Z
49%: B, C, ... Y, Z, A
51% (i.e. a narrow majority) rank option A top and the other 25 in order, B-Z. The other 49% rank A as the worst (26th) option, but otherwise B-Z in order, 1st-25th. Here majority rule chooses A, which gets 51% of the vote to B’s 49%. A does not, however, maximise the total amount of good, because although 51% of people get their most-preferred option, the other 49% get their least-preferred[7]. Surely B would be better – first choice of 49% and second choice of the rest. This is the case in favour of the Borda count. The Borda count takes second-, third-, etc-preferences into account, as a proxy for intensity.
The problem with this method (assuming it’s trying to maximise utility, as described) is that it uses an ordinal ranking as proxy for intensity, when what’s really needed is some cardinal measure, that reflects the fact that, for a given voter, there may be a larger gap between A and B than B and C. We can see the problem with another example. Suppose an election consists of one conservative (right-wing), a communist (extreme left) and an extreme socialist (not quite as far left as the communist)[8]. Here, there’s very little difference between the communist and extreme socialist – many of those who vote for either might be almost indifferent between the two. Simply representing the voter’s rankings as (2, 1, 0) doesn’t reflect how much he prefers one to another, when on a cardinal scale it might be (100, 5, 4) if he was a conservative, or (10, 9, 1) if left-wing.
The Condorcet problem faces a similar problem. Pairwise comparison may find the extreme socialist wins over both the communist and the conservative. Nonetheless, while the extreme socialist may be the closest candidate to the median voter, he may be considerably to the left of that voter’s ideal. That is, he may simply be the ‘best of a bad bunch’. Similarly all the conservative-voters will presumably choose the socialist over the communist (unless being strategic), but that doesn’t mean they really endorse him[9]. It’s likely there will be a considerable range between the conservative and communist in which one could win the election either side of the median voter’s ideal. In a perfectly competitive (electoral) market, one might expect parties to converge on the median voter, but this needn’t happen if they have no more information than the votes, which simply won’t reveal that the median voter’s ideal is for (say) a left-of-centre administration, only that he voted for an extreme socialist.
The example is more problematic for the Borda count, however, because it raises another – perhaps the most fundamental – problem with it, the fact that its results depend on the number and range of options. Suppose, for example, a number of ‘blanks’ were added, to allow voters to more accurately represent their cardinal preferences[10]. These blanks would change the scores, and possibly the outcome. The same would happen if another genuine candidate, on either side, were to stand – e.g. another on the far right would (presumably) favour the conservative.
I don’t have a problem with the fact that Borda count fails independence of irrelevant alternatives per se, but I do think it’s problematic both that it still fails to reflect cardinal comparison and that because its result depends on the number and range of options it is manipulable. Candidates on one side of the spectrum are generally advantaged by more others standing on their side. The logical result would be everyone standing. If nothing else, it makes a complete ranking almost impossible for individual voters.
The Condorcet system isn’t as vulnerable in this respect. Admittedly it can fail to represent whether a candidate is really approved of, or just the best of a bad bunch (as in the above example). Condorcetians, however, might welcome extra candidates. E.g. suppose a left of centre candidate was to stand in the above case. It’s not guaranteed that he’d be a Borda winner, but very likely he’d be a Condorcet winner. The other major problem with the Condorcet method is that there need not be a Condorcet winner. This may be resolved by using the Copeland rule, as above.
Both methods have an understandable rationale in trying to count all of a voter’s preferences, and thus find a candidate acceptable to all. Neither, I think, fully succeeds, and both make a high demand on voters (expecting them to completely rank or compare candidates). I think the best method to use will depend on the context[11]. If the system is ‘open’ to new candidates/options coming forward, then the Condorcet (or Copeland) criterion will probably fare better, as it will avoid easy manipulation. On the other hand, once options are fixed, the Borda count may be better as it is likely to better reflect cardinal utilities than simple pairwise comparison.
[1] Quoted McLean and Urken (1987) Classics of Social Choice p.18
[2] The Copeland score is a measure of how many majorities each wins. Note in the previous example, each option has a Copeland score of one, so this still isn’t decisive. If there are more options, however, we may get a>b and a>c but a
[3] McLean and Urken (1987) p.34.
[4] Quoted McLean and Urken (1987) p.34.
[5] Consider a choice between cheese or tuna salad in a restaurant. If someone chose cheese, but changed their mind to tuna on being told chicken was also available, we’d certainly think it odd…
[6] Shepsle & Bonchek (1997) Analyzing Politics: Rationality, behavior and institutions pp.167-72.
[7] In a vote between A and B, this represents the case where an almost indifferent majority (the 51% that barely prefer A to B) out-vote what is presumably an intense minority.
[8] I assume a simple left-right economic dimension and single-peaked preferences.
[9] In this case, approval voting would seem attractive – presumably those on the right will only endorse the conservative, while many on the left will endorse both communist and socialist.
[10] E.g. ‘conservative, blank, blank, blank, socialist, communist’ or ‘socialist, blank, communist, blank, blank, conservative’.
[11] It could be said this is a principal lesson of social choice theory – that electoral/voting systems are not fixed, but tools, for us to use when and as appropriate for what we want.
Thursday, October 20, 2005
Busy
Wednesday, October 19, 2005
Anderlecht 0-1 Liverpool
I wasn't able to watch much of the match, though I went to a pub to discuss Parfit's Reasons and Personswith some friends and the second half was on screen. Pleasing to see Cisse score another. No coincidence we score more with him in the team, and I hope he now hits form... Also good to see Kewell make a competitive comeback, though I didn't see much of him in the game. I'm really looking forward to having him fit and in the team again.
Tuesday, October 18, 2005
Fixture Congestion and CL
I'll admit, Liverpool did suffer in both League and FA Cup as a result of not being strong enough to compete on four fronts, but their success clearly demonstrates European progress is possible - it's just a matter of priority. SAF has never treated either domestic cup as a priority, so shouldn't worry about those (even if - like the last two seasons - they may be his best chance of silverwear). The problem last season was fielding a weakened side in the group stage once they'd qualified, thus finishing second and facing AC Milan in the first knockout round.
Designer Baby Debate
As usual, I was slightly disappointed. Of course, one can’t expect rigorous philosophical argument from debaters, but few were particularly inclined to grapple the issue at hand, viz. the proposition ‘this house would design a baby’.
That motion is quite distinct from ‘this house would allow others to design babies’. It doesn’t assume the Union debating chamber has become parliament, and is in chance of legislation. It concerns a personal moral decision. If I asked my students ‘would you design a baby?’ and ‘would you legalise designer babies?’ I’d expect very different arguments. The latter wasn’t really the topic – though unsurprisingly it was what many debaters focused on – perhaps because it was more interesting, or simply a tendency to see many evaluative claims in terms of legislation. (A mistake Jeremy Waldron diagnoses in his article ‘What Plato Would Allow’, Nomos XXXVII Theory and Practice, I. Shapiro and J. W. DeCew eds.)
Moreover one opposition speaker focused his argument solely on technological limitations. Not the fact there are unknown risks with current science (which isn’t decisive either way – there are risks to not improving, like bird ‘flu), but rather the simpler claim that we shouldn’t design babies because we can’t.
On the surface, this is a valid application of ‘ought implies can’, which is widely (not universally) accepted. If you can’t do something, it doesn’t make sense to say you ought to. However the motion didn’t say we ought to design babies – only that the house would or (to permit the legislative interpretation) would permit it. There’s no reason not to permit something we can’t do – why should I ban you from flying under your own power? On the assumption a liberal government should allow as much as possible, it seems this is a reason not to implement a ban…
In any case, I took offence to this line, because it depends only on current technological limits. The really interesting question is the normative one, and I hope I don’t say that just because I work in political/moral philosophy. Scientists tell us what we can do, but it requires others – whether just ‘experts’ or the wider public – to tell them what we should do. One thing we could do, for example, is launch a nuclear missile – that we can says nothing about whether we ought to.
Admittedly the normative debate only becomes practical once the science is possible, but that’s no reason not to enter the debate now – for aside from anything else, our conclusion will affect the development of science. IF the only reason not to design babies is that we can’t currently, then presumably we should increase research until we can, and then go ahead with it…
Sunday, October 16, 2005
Liverpool 1-0 Blackburn Rovers
Ok, it was only 1-0 but Liverpool dominated possession, as once Blackburn were down to ten men they were bound to defend for a point. While it’s true Morientes and Cisse both missed loads of chances, that proves we were creating them.
Don’t get me wrong, I’m not over-joyed by our performance, but the important thing is to win. Last season I believe we only drew, so this is two more points gained, and means we have ten compared to five from equivalent fixtures last season. Not bad!
The main talking point would probably be Hyypia getting axed from the squad. Well, I said we needed a first choice replacement in the summer, and given the way Drogba ran rings round him last week I wasn’t too surprised. That he wasn’t even on the bench was a bit of a surprise – unless he’d picked up a knock and wasn’t considered fit.
The formation was a bit of a strange one. Either Josemi or Traore (or both) could play CB, and Warnock or Finnan could play in midfield. Initially it looked like perhaps we were playing a back three and wing backs – something else I’d called for, albeit with Finnan and Riise. Perhaps in fact it was Josemi (RB), Carra and Traore, Warnock (LB) and Finnan (RM) in a 4-4-2.
The decision to play Cisse as a second out and out striker seemed to work. Granted his goal was only from a free kick, and he missed other chances, but he looked far more of a goal threat than Crouch. I’d like to see us playing two up more often, though arguably we were only freed to do so by Gerrard’s injury. That also gave Zenden the opportunity to play in the middle, and he had possibly his best game yet for us (not that hard)
Friday, October 14, 2005
The Complexity of Majority Rule
1. Is majority rule a good idea? Why is it more complicated than it looks?
To understand whether majority rule is a good or bad idea, we need to understand it in its full complexity. Therefore I propose to tackle the two questions in reverse order. That is, I begin by raising reasons why majority rule is more complicated than it appears to many casual observers, then (drawing partly on this analysis) argue that it is not a good idea.
When people refer to ‘majority rule’, they generally have in mind democracy (= rule of [all] the people),[1] and the assumption that when the people disagree then the decision of most must pass for that of all. As Locke says:
“[W]hen any number of men have, by the consent of every individual, made a community, they have thereby made that community one body, with a power to actIn fact, matters are more complicated than this. For a start, most people fail to distinguish an absolute majority (50%+1), from a relative majority (plurality), which is simply more than any other option – and could be as little as (v/n)%+1.[3] An absolute majority is a more convincing mandate, but is only guaranteed when there are just two options (and an odd number of non-abstaining voters). The British ‘first past the post’ system elects MPs on the basis of just a relative majority, e.g. in 2005 Clwyd West returned a Conservative MP with just 37.2% of the vote.[4]
as one body, which is only by the will and determination of the majority. For that which acts any community, being only the consent of the individuals of it, and it being one body, must move one way, it is necessary the body should move that way whither the greater force carries it, which is the consent of the majority, or else it is impossible it should act or continue one body, one community, which the consent of every individual that united into it agreed that it should ; and so every one is bound by that consent to be concluded by the majority. And therefore we see that in assemblies empowered to act by positive laws which empowers them, the act of the majority passes for the act of the whole, and of course determines as having, by the law of Nature and reason, the power of the whole”[2]
The resulting composition of parliament was that Labour won 358 seats with just 35.3% of the national vote, while the Conservatives took almost as many votes – 32.3% - but won only 198 seats.[5] This is by no means an anomaly. In 1874, 1886, 1895 and 1906 UK General Elections produced a landslide of seats for one party that was based on system bias, not popular vote.[6] Nor is it confined to the British case. Abraham Lincoln won a majority in the Electoral College with less than 40% of the popular vote in 1860.[7]
It seems sometimes institutions must be used to create majorities. There may simply be no other obvious way of identifying what ‘the majority’ want, e.g. Condorcet’s majority-cycling.[8] One problem with this, however, is that different institutional rules produce different outcomes. It’s then the institution that determines the outcome, not the preferences of people in society. This isn’t what we allegedly want!
A related problem occurs when there are more than two options. As I said above, an absolute majority is only guaranteed in this case. When there are more options, particularly on two dimensions, the formation of a majority is complicated, and depends on institutions. For example, the extension of the franchise in the UK – it could be extended to all men, to women of the same property qualifications as men, or both. That is, there were four options[9]:
A Limited male franchise; Male only franchise
B Limited male franchise; Give women the vote
C Extend male franchise; Male only franchise
D Extend male franchise; Give women the vote
A majority might prefer D to the status quo (A), but if motions are considered separately for female or wider male franchise they may still lose. If all four options are considered together, matters are even more complicated.
One thing many electoral systems try to do is artificially reduce choices to binary. According to Riker, there is no fair way of doing this. Certainly there is no neutral way – the reason a plurality run-off and sequential run-off produce different ultimate outcomes is that they proceed through the elimination differently. The below example[10] features 55 people, in six groups, and shows how six seemingly reasonable procedures each give different results over their preferences A-E.
I (18 people): A D E _ C B
II (12): B E D _ C A
III (10): C B E D _ A
IV (9): D C E _ B A
V (4): E B D _ C A
VI (2): E C D _ B A
Each group (I-VI) includes the number of people in brackets. The underscore marks the acceptance point – the group accepts all candidates above (to the left of) this. Thus six procedures give different results:
Method: Winner
How it works
Result
Simple plurality: A
A vote is held with all five options. The option with the most votes wins. (This is like our current first-past-the-post system).
A wins, with 18 votes (options B-E scoring 12, 10, 9 and 6 respectively).
Plurality runoff: B
Here a first-vote is taken as above. Instead of declaring a winner at this stage, the two with most votes enter a second-ballot. Now there are only two options, one should win a majority – though voters won’t necessarily be voting for their first-preference. (This is like French presidential elections).
Here, we see A and B make it to the second round. Here, however B has 37 votes (12+10+9+4+2), beating A’s 18 – so B wins.
Sequential runoff: C
A vote is taken of all five. The least popular (e.g. E in the first-round) is eliminated. The process is repeated with four options, again eliminating the least popular. This is continued until there are two options – the least popular is eliminated and the other wins.
E is eliminated in the first round with just 6 votes. These are redistributed to B and C (the second-preferences of those voters). Thus D goes at the next round, and those votes are also redistributed to C. At the third-vote, A has 18, B 16, and C 21. Thus B goes. The final vote is between A and C, and C wins 37 to 18.
Borda count: D
As described above, each gets four points per first-preference, three points per second-preference… to zero points for a fifth (last) preference.
D gets 136 points = (18x3)+(12x2)+(10x1)+(9x4)+(4x2)+(2x2). This wins. A gets 72, B 101, C 107 and E 134.
Condorcet: E
The Condorcet method identifies if one option is a ‘Condorcet winner’, that is, beats every other option in pairwise comparison. There are fifteen ways of pairing five options. Each option is therefore pitted against each of the other four individually. If any option wins each of those four comparisons, it is declared the winner. (This method has nothing to say if there is no Condorcet winner – e.g. in the majority-cycling case).
Here E wins. E beats A 37-to-18, B 33-to-22, C 36-to-19, and D 28-to-27.
Approval voting: D and E tie
In this system, everyone casts a vote for each option they consider ‘acceptable’. They can have as many or as few votes as they like. The option ‘approved’ by the most people wins. (Note: if everyone ‘approves’ only their first-preference, this is equivalent to plurality-vote).
The empty cells above illustrate the ‘approval threshold’. All the voters approve their top three preferences, except group III (who approve their top four). A is approved by 18, B by 26, C by 21, and D and E by all 55. Thus D and E tie.
What we see here is that, even given full information about voters’ preferences, it’s not obvious which option should be declared the ‘winner’. Note the procedures here aren’t, of course, simple majority-rule. None of the five options commands a majority (at first). Although the Borda count and approval voting aren’t directly related to majority-rule, the other methods are all attempts at capturing its essence. The plurality-vote is a weaker approximation of majority-rule, requiring only a ‘relative’ majority. The plurality and sequential run-off methods are both ways of whittling options down to two, so majority-rule becomes applicable. The Condorcet method employs majority-rule in a series of two option comparisons.
The ‘majority’ that rules is, it seems, largely arbitrary and meaningless. Moreover, it is not just that one possible majority is selected (at random) by the system, instead the system ‘creates’ majorities where none existed before. For example, by narrowing a four-way contest down to a two-horse race, it means one party must have a majority, but this doesn’t mean they have the real support of 50%+1 – as many of those would really have preferred another candidate, and hence another electoral system that gave their preference a chance.
Representative systems typically illustrate the creation of majorities in another way. A majority of representatives need not represent the majority of the larger population. In theory, 50%+1 of the MPs could’ve each been narrowly elected in their constituency – by just 50%+1 of voters, in each of those 50%+1 constituencies – and thus speak for little over a quarter of the population. The other almost 75% of the population could be against a motion passed by the majority of MPs![11] Which majority should rule?
If majority rule seems meaningless, then it’s hard to argue that it is a good idea. Epistemic democrats (e.g. Rousseau, Estlund) argue the majority are our most reliable guide to the ‘right’ outcome. This not only assumes one uniquely right outcome – controversial in modern heterogeneous democracies – but also that voters reach independent judgements and have a greater than 0.5 chance of being individually right on any particular issue. These assumptions are, if not downright unrealistic, controversial.
A utilitarian justification for majority rule is likely to proceed in terms of it being ‘better’ – which need not make the assumption it is better for everyone (like Rousseau’s General Will), it can appeal simply to the net sum of satisfactions. As Sen has argued, however, preference-satisfaction is an inadequate measure of well-being.[12] In any case, there is not enough information revealed in voting to guarantee that utilitarian optima are reached. Majority rule, for example, allows an almost indifferent majority to prevail over an intense minority, when the reverse would bring about greater net satisfaction.[13]
Even if we assume that people are better off if they get their way, and that more people getting their way is socially better (i.e. a greater net satisfaction), repeated majority rule may produce repeated winners and losers, which may violate notions of fairness. For example, in a district split 51/49 (in some permanent way, e.g. along race lines), the 51% will get their way 100% of the time, which hardly seems fair. They could, for example, decide to enslave the others.[14] Even if a new vote was taken each week on who were to be slaves and who masters, the 51% would win every time!
Sometimes majority rule may seem natural and appropriate; for example, if there is a one-off binary decision to be made where each has an equal stake. It certainly does not guarantee right, good or fair outcomes, however – probably no procedure can. Moreover it is dogged by problems of defining ‘the majority’, which is often more an artefact of the electoral system, rather than a real reflection of people’s preferences. As such, it struggles when there are more than two options or one dimension of issues, as revealed by majority cycling. One cannot assume majority rule is a good idea in all contexts.
Thankfully there are alternatives to majority rule that treat each equally. The appeal of lottery-voting was illustrated to me by an actual case arising in our GCR – and I’m certainly not the first to be stimulated by college politics.[15] In Trinity 2004, there was a proposal to buy some reference books,[16] but there were a range of views on what to do – some wanted top-of-the-range books costing £200, others to reject the motion altogether and most in between – a reference library but at a lower budget. The outcome seems to depend more on decision mechanism than preferences. E.g. one might write down how much everyone would spend and take an average (presumably more than £0 but less than £200). Or set several options (£0, £50, £100, £200) and have people vote which. Even that could use simple (relative) majority or some means of alternative voting (like our GCR elections). Or have a yes/no vote followed, if applicable, by decision over how much to spend (perhaps simply a high/low choice) – or the reverse (set a hypothetical amount, then decide whether to spend it).[17]
In these situations, any ‘majority decision’ will either fail or succeed only due to the voting mechanism. There’s a case for taking an average, which minimises aggregate dissatisfaction (how far each voter’s preference is from the outcome). This makes majorities always hostage to minorities; if 99 people want nothing spent, but one person £200 they still have to spend something (£2). Strategic voting presents another problem – if one wanted £50 but thought most people inclining to £0, one might vote £200 thereby bringing the average artificially closer to one’s preference.[18] Finally, averaging won’t work in cases where what matters more is polarity (which side of the issue one falls on) rather than how far from the middle one is – e.g. the abortion debate (a moderate pro-choicer may have more in common with a radical than a moderate pro-life campaigner)[19]
While acknowledging other procedures may produce a better outcome, I think fairness is satisfied by a ‘random dictator’ model – everyone writes down how much they would spend between £0 and £200 and one choice is selected at random as group policy. This gives everyone an equal chance and respects numbers – if more people favour a particular option (say £100) that becomes more likely – and not just numbers who exactly agree, but those who are close (e.g. someone who wanted £90 isn’t so far from £100).
Of course, this proposal has its own problems – e.g. one outlying voter may be drawn, and the result obviously depends on the institution (which vote is actually drawn) rather than just votes – but each option’s chances are improved by each vote they receive.
Notes
[1] As Aristotle noted, this isn’t necessary. Even oligarchies operate by majority rule, so what distinguishes democracy is the franchise.
[2] Locke Second Treatise of Government para.96. Various editions, e.g. Two Treatises on Civil Government with an introduction by Henry Morley (London: George Routledge and Sons, 1884) p.241. I am not the first commentator to find this unconvincing. See, e.g. Gough (1950) John Locke’s Political Philosophy pp.60-63 and Simmons (1993) On the Edge of Anarchy: Locke, Consent and the Limits of Society p.92ff.
[3] v = voters, n = options. If there are 100 voters and four options, 26 votes could be a ‘relative majority’ (if the others are split 25, 25, 24).
[4] Labour 35.9%, Lib Dem 13.3%, Plaid Cymru 10.9%. Source.
Note this also neglects the further complication that turnout was only 64%. Even an absolute majority of those that vote need not be even a relative majority if everyone voted. This is a problem if abstention rates differ between those of different political views, as is likely given that members of poor, disadvantaged minorities are generally less likely to vote.
[5] Source.
[6] McLean (2001) Rational Choice & British Politics p.91.
[7] McLean (2001) Rational Choice & British Politics p.13ff; c.f. McLean (2002) ‘Review Article: William H. Riker and the invention of Heresthetic(s)’ British Journal of Political Science 32 pp.550-3. Note this is complicated by the two-stages of indirectness, which I come to later.
[8] For example, if three people rank options a>b>c, b>c>a and c>a>b then one a first-preference count each option gets one vote, and in pairwise comparison a beats b (2-to-1), b beats c and yet c beats a. The usual solution is a status-quo bias, which is non-neutral and effectively makes one person a dictator (if c is the status quo, person three gets what he wants, though everyone else prefers b).
[9] From McLean (2001) Rational Choice & British Politics p.106.
[10] Originally owing to Malkevitch; reproduced from Shepsle & Bonchek (1997) Analyzing Politics: Rationality, behavior and institutions pp.167-72.
[11] For example, suppose there are five districts, each of 20,000 voters, and each represented by one legislator. Even though there is not one majority-bloc, it may still be that a majority within three of the districts – who are not a majority overall – are sufficient to pass bills affecting the whole polity. It takes only three of the five legislative votes to enact policy. Each of these three legislators could’ve been elected by a narrow majority, however – say, just 12,000 of their 20,000 constituents. In this case, 36,000 voters strategically placed effectively determine policy for the whole 100,000. The other 64,000 may all be opposed – but they win just two districts with over-whelming majorities (indeed, a unanimous 20,000 votes) and lose the crucial three 8,000-to-12,000. This effectively violates anonymity. See Still (1981) ‘Political Equality and Election Systems’ Ethics 91:3 [Special issue: Symposium on the Theory and Practice of Representation] p.382.
[12] His famous examples include a contented slave and a housewife who accepts repression. The danger here is not an outside influence prevailing over their preferences, but shaping their preferences.
[13] The Borda count is an attempt to consider intensity of preferences, but even this fails as it uses an ordinal ranking rather than a cardinal one. Consider the case where there are five options for the income tax rate – 65%, 64%, 63%, 62% and 30%. Someone who ranks them in descending order (65-30) is presumably much more satisfied by his ‘second preference’ than someone who ranks them in the reverse order (whose ideal is 30%, but whose ‘second preference’ is 62%).
[14] Of course, one who thinks there are values prior to the democratic process – as one must, I think – can always think a majority wrong, as with any other decision procedure. Perhaps constitutional protections can be used to block some infringements of a minority’s rights, but the problem persists in essence even if what is decided is something less important – like a number of economic decisions that all benefit the majority.
[15] So was Dodgson in Christ Church – see McLean and Urken (1995) Classics of Social Choice p.52. Many others have come from similar small groups, e.g. the Paris Academy or church groups.
[16] Lengthy debate was involved in the first meeting of Trinity Term 2004 before a rather vague motion was thrown out. A refined motion was subsequently passed in the second meeting of term. This discussion draws on my communication with the GCR president, particularly an email of 28th May 2004.
[17] If we decide to buy books, then settle the amount, presumably many who’d been opposed to the purchase would then support buying the cheapest books. This is not guaranteed however – some may prefer we didn’t buy books, but if we were going to we ought to get good ones. (This is one factor complicating the ‘aggregation’). If we decide on the amount first, it’s perhaps more likely those opposed to any purchase would go for a higher figure, if they think this will swing other voters (who want cheaper books) into voting against the purchase altogether. (Again, they might in fact decide on a lower price, if they think that will be more effective in encouraging people to vote against the purchase – the majority believing cheap books aren’t worth having, for example).
[18] I owe this point to Toby Ord. One of the advantages of lottery voting is that it encourages true preference reporting.
[19] We can’t assume averaging best in the book example either. £2 would only buy a very cheap dictionary – those who opposed buying anything may see that as literally ‘worse than nothing’ and prefer that if we bought anything it should be of reasonable quality.
Tuesday, October 11, 2005
Two Tests - IQ and Jurisprudential Orientation
In any case, it's one you can do without flashy graphics. It's one of those 'ferrying people across a river' type things, with some restrictions on who can go where.
There's a family of six (Mother, Father, two sons, two daughters) and a policeman and thief who must all cross a river on a two-person raft. The following rules apply:
Only 2 persons on the raft at a time.
The father cannot stay with any of the daughters without their mother's presence.
The mother cannot stay with any of the sons without their father's presence.
The thief cannot stay with any family member if the Policeman is not there.
Only the Father, the Mother and the Policeman know how to operate the raft.
The solution is available here.
Another interesting test I found today is one that determines your jurisprudential orientation - i.e. whether you're a positivist, Dworkinian, etc. It's available here.
For the record, I think I'm confused. Maybe more regular attendance at the Jurisprudence Discussion Group in question will help...
Sunday, October 09, 2005
What's a PhD Worth?
I was slightly perturbed by reading this article that seems to question the value of a PhD, arguing they tend to focus too much on small pedantic issues and lose the big picture. While a lot of my professors don’t have PhDs, that’s the case of a past generation – now it’s a prerequisite of most academic jobs, though of course I do know one or two exceptions (Andrew Williams, for example, never actually completed the D.Phil he started here, with my supervisor).
If my research goes well, I’d like to enter academia. I am aware how competitive it is though. This report highlights that there are more doctors than academic posts, even if the government’s university target might increase demand for lecturers.
One advantage of doing politics rather than philosophy (at least when it comes to the official label of my thesis, which falls between the two really), is I suppose it sounds more marketable to potential employers such as newspapers or think tanks. Another Guardian article emphasises the need to look for transferable skills that can be applied outside of the academic ‘ivory tower’. I’ve already attended numerous applied ethics seminars while doing my masters, and plan to follow these up by attending the Public Policy Unit lunchtime seminars this term – so I hope I’m doing enough to keep that route open.
At the end of the day, a lot of people don’t even get as far as doing a PhD – much less finishing – so I suppose I’m lucky to be here, and funded. Being paid £12,000 just to be a student for two more years isn’t such a bad deal after all…
Saturday, October 08, 2005
Dinner Parties and Dreams
We went for a huge vegetable stir fry followed by apple pie, fruit and ice cream, which went down pretty well. We’d over-estimated on some of the ingredients, so I have plenty of leftovers (since it was my flat) – on the other hand, I have most of the clearing up to do…
Since everyone else was also having a dinner, we went over the communal recreation area to carry the party on until around 1-1:30am. Someone then decided to invite everyone back to their flat, but I decided I’d had enough by then. Once I’d done some clearing up, it was 3am before I got to bed – and I have a joint birthday party to go to tonight too…
I was up around 8am, to go to the toilet, then went back to bed. I don’t know if you ever get this, but then I had a really weird ‘dream’. I don’t know if it counts as a dream, because technically I think I was probably still awake – but just kind of half-asleep, dozing and with my mind wondering.
I read an interesting piece on dreams the other week, but I don’t usually remember mine (unless I’m somewhat awake, like this) so I thought I’d describe it. If anyone has any ideas what it might mean, feel free to comment…
I was in the Bodleian library, though not a part I’d ever seen before. I was half-reading something, but ended up paying more attention to Fiona and Nick (who I’d been talking to last night, and who were sat at the same table) – they were trying to explain what a ‘concept’ was to one of Fiona’s friends, who just didn’t get it.
Somehow we went from there, to me being in bed (half-asleep, as I was in real life), but Nick and Fiona still there continuing the conversation. Feeling the need to wake up I (in my dream) pulled open my bedroom curtain. Having done so, I saw what I thought was a plane doing stunts (rolls, etc) in the air, but coming down as it did so. As it got closer, I realised it was actually a space shuttle (like Discovery etc), and it actually came down – landing upside down in the Thelwall House garden (visible rom my flat, only a few hundred yards away). At that point, I got up, pulled on my dressing gown, and started heading for the scene, trying to ring 999 and Leigh (an astrophysicist, who lives in Thelwall) on my mobile.
Odd huh? After that though, I really got up. It was about 10:30am, and I have a lot to do – not least clearing out the ‘spare’ room in our flat, because my third and final flatmate Pavel’s coming back from his fieldwork in Prague today.
Friday, October 07, 2005
Blog Plugging
Nonetheless, a few others have come to my attention. I started here after seeing a blog by my friend Rob (who did the M.Phil Political Theory with me). He's got many links and suggestions, so that also took me to an interesting one by Chris Brooke (an Oxford politics/history tutor at Magdalen).
I've linked to these in the side bar, under 'other blogs I read' (though it'd be an exaggeration to say I'm devoted to them). I'll keep that up-dated if and when I stumble across more things of note.
Thursday, October 06, 2005
The Perfect Boyfriend and the Ontological Argument
However, because “not everyone’s perfect” (by which I think they mean no one’s perfect – actually a completely different thing) they decided he had a ginger mullet. Someone else remarked something like “surely "not being real" is enough of a disadvantage to make him not perfect to start with, without him even needing the ginger mullet?”
This reminded me of the ‘ontological argument’ employed by the likes of St. Anselm and Descartes in an attempt to prove the existence of God. The gist of the argument is that God is by definition all perfect. If existence is a perfection (the controversial bit implied above) then God by definition exists - because whatever you could imagine with properties x, y, z would be more perfect if it had x, y, z + existence.
The problem with this is that the argument is supposed to run:
'God is all perfect'
'all perfection includes existence'
therefore 'God exists'.
The first premise, however, is slightly ambiguous, but effectively presupposes God's existence - that is, it's taken as 'there is a God who is all perfect'. If the argument is made explicitly hypothetical, it doesn't reach the conclusion. It should be:
'if there's a God, He is all perfect'
'all perfection includes existence'
therefore 'if there's a God, he exists', which is obviously less interesting...
Similarly if there is a perfect boyfriend, then he exists (because an imaginary one is obviously less than ideal), but one can’t suppose from the outset that a perfect boyfriend does exist and argue from there. The same would hold, of course, for girlfriends.
Actually, it reminds me of a joke about the perfect (husband-material) man:
Recently a "Husband Store" opened where women could go to choose a husband from among many men. It was laid out in five floors. The only rule was, once you opened the door to any floor, you HAD to choose a man from that floor; if you went up a floor, you couldn't go back down except to leave the place, never to return.
A couple of girls went to the shopping center to find some husbands...
First floor The door had a sign saying, "These men have jobs and love kids." The women read the sign and said, "Well, that's better than not having a job or not loving kids, but I wonder what's further up?" So up they went.
Second floor The sign read, "These men have high paying jobs, love kids, and are extremely good looking." "Hmmm," said the ladies, "But, I wonder what's further up?"
Third floor This sign read, "These men have high paying jobs, are extremely good looking, love kids and help with the housework." "Wow," said the women, "very tempting." But there was another floor, so further up they went.
Fourth floor This door had a sign saying "These men have high paying jobs, love kids, are extremely good looking, help with the housework and have a strong romantic streak." "Oh, mercy me," they cried, "just think what must be awaiting us further on!
So up to the fifth floor they went. Fifth floor The sign on that door said, "This floor is empty and exists only to prove that women are impossible to please. The exit is to your left."
Wednesday, October 05, 2005
Birthdays and freshers
I must begin by saying happy 21st birthday to my brother John. I don’t know what he’s up to, but he’s in his final year at university, and no doubt has plans to go out drinking…
In fact, that’s not so different to what the week’s been like here. Yesterday I had tea with the chaplain, followed by formal hall in our ‘families’ (according to the graduate parent/adoption scheme) and a ghost tour of Oxford. It was pretty interesting, though I don’t really believe any of it.
The undergraduates came back to college today too. We know better, but they think they own the place; and it's strange having so many people about again just when we'd got used to things being so quiet. It's funny how you forget what it's like to start university in a new place. Even their questions are so funny - 'are you a second year?' 'No, fourth'!
Other than that (or, indeed, including it) today was rather boring – I had to get some work done, and I have a teacher training seminar to attend tomorrow. I did actually get a (mass) email after people to tutor Mill’s Utilitarianism to first year undergraduates. I expressed an interest, but haven’t heard anything, so that looks unlikely.
Sunday, October 02, 2005
Brunch, Liverpool 1-4 Chelsea
The main event of today was a brunch in college. It was absolutely packed – we have a huge intake of graduate freshers this year – 66 – which not only meant we had to go for more food but the room was too full to circulate properly. I didn’t really talk to as many people as I should have, but I did meet the other two of my ‘children’ (from the college parenting scheme).
After clearing up, I was ready to come home only to find the bike I spent £150 on yesterday had a flat tyre! It must have been punctured when I bought it, because the guy in the shop pumped it up, and I only rode it from there to college (10 minutes) It meant I had to walk it home (30 mins) and will have to take it back tomorrow for repair – which I hope they’ll do free…
In consequence, I missed the first half of Liverpool v Chelsea, coming in to find it was 1-2. The final score was a rather embarrassing 1-4 to Chelsea, particularly disappointing given how we pretty much dominated the game on Wednesday…
I’m not sure I can comment on the performance too much (or Lampard's crowd incitement), but looking at the statistics, I don’t think we deserved such a heavy defeat:
Possession: Liverpool 55% Chelsea 45%
Shots: Liverpool 12 Chelsea 7
Corners: Liverpool 5 Chelsea 2
I was pleased to see Rafa had the guts to make bold substitutions – e.g. Pongolle for Hyypia. Unfortunately this time it didn’t came off – we got hit on the break, and the scoreline suffered. Still, losing 4-1 isn’t much worse than 1-0 (like last year). No points from this one again, but we are still up on last year.
People already calling for Rafa’s head are lacking perspective – but I admit we do need to start winning, and soon… YNWA
UPDATE: Some further thoughts…
I’ve seen highlights on Match Of The Day 2 now, so I can add a bit more. I wasn’t impressed with their analysis really, though Graeme Le Saux did show how much Chelsea rely on the long ball to break. There was no comment on the penalty, where Traore did take the ball (and man). Granted a needless and stupid lunge, but Liverpool have been denied clearer penalties against Chelsea in the last few games.
Shame Reina couldn’t demonstrate why he won a reputation for penalty saving in Spain, but he got close. Lampard rightly I think book for inciting Liverpool fans after scoring, but no need to make a bigger deal of it than that.
I can’t complain too much about the other goals. Three and four were clearly on the break – well perhaps the latter only came from a throw conceded because of a foul on Pongolle, but never mind we were a shambles at the back (not surprising with Riise and Alonso pretty much filling in for Hyypia and Traore) – but of course there would’ve been a very different complexion on the match if we weren’t trailing and trying to come back.
To their credit Chelsea played some good football, and Drogba actually looked like the one who played for Marseille, not the £24m misfit he normally has in a Chelsea shirt. Perhaps they deserved the win, but I still say the scoreline flattered. In five meetings last season and one last week, there was never more than a goal in it, and that pretty much reflects how close these teams are in a one-off match. (Granted Chelsea’s greater league consistency – which comes easily when you have such a large and expensive squad)
Oxford Street
I walked most of the way to Oxford station, stopping only to buy a much needed new bike now I’ve had a bit of money come in from work… Just made it to the station at 10:30 to get what I thought was the train I wanted, but it turned out to be a slow one. Took me one hour forty to get to Paddington – which would’ve been just 55 minutes on a fast train, and probably shouldn’t have been that long even with the stops (we sat stationary in Didcot for ten minutes!)
Made it to my great aunt’s not too late, and we went to a nearby Italian for lunch. It was quite nice, but the portions were fairly small and for four of us (main courses, two side salads, three desserts and mineral/tonic water to drink) it cost £70!
Got to do a bit of shopping on Oxford Street afterwards. I bought a few more CDs in their HMV – though it either didn’t have such a big clearout as the smaller Oxford store, or the best bargains had gone.
Highlight of the day was the fact that I passed Martin Grech on Oxford Street. I wouldn’t have recognised him, were it not for the fact I saw him live a week ago, but I’m sure it was him. I didn’t notice until he’d almost passed, otherwise I might have said something – but then, I’d only really have said ‘wow, you’re Martin Grech’ and given that he seems quite shy it might’ve been awkward…
Freshers week officially begins tomorrow, but I’m going to a ‘back to school’ party tonight to kick things off. If it’s anything like last year’s party it’ll be great fun, though I’ve been on my feet all day and don’t feel much like dancing to be honest.