Condorcet and Borda Voting Methods

Continuing my series of voting theory papers. Don't worry, it's a bit shorter than last time, though it is a bit more technical...

Although the modern ‘social choice’ literature began with Duncan Black in the 1940-50s, major discoveries were originally made – and lost – much earlier, for example by Charles Dodgson (Lewis Carroll) and, most significantly for present purposes, by Borda and Condorcet in the late 18th century (1770-80s). Borda and Condorcet proposed two voting rules now generally known after them, though in fact both may have been anticipated before (even if they were unaware of the fact).

Ramon Lull in his novel Blanquerna (1282-7) proposes a procedure to select two candidates from a larger group. A cell has to be drawn featuring the possible combinations, as illustrated:

Assuming there is no positional element (1st and 2nd) there are 21 possible combinations for choosing two from seven, e.g. A and B (which is equivalent to B and A). Cells marked X are ineligible for votes, as A can’t be compared with him/her-self. The other cells can be used to compare each possible pair, e.g. A against B, A against C, … B against C, etc. The result is a comprehensive pairwise comparison, and Lull’s conclusion is that “the candidate to be elected should be the one with the most votes in the most compartments [cells]”[1]. Unfortunately, ‘the most votes in the most compartments’ is ambiguous. It could mean either each candidate’s total votes (from all cells) are added up, in which case the procedure is equivalent to the Borda count. Alternatively one could simply focus on who wins the most majorities from pairwise comparison – i.e. the Copeland rule, a natural extension of the Condorcet procedure (to which I’ll return later). Despite Borda citing Lull in support of his method, it isn’t actually clear which of these interpretations is correct – nor does it matter greatly to our present attempt to adjudicate between the two.

Borda proposed a rank-order count in 1770. According to this procedure, each elector orders all the n options. First preference is given n-1 points, second preference n-2 and so on down to last (least preferred), which gets no points. The winner is the option with most points. Condorcet proposed a system somewhat like Lull’s, where each option is compared to every other in pairs. A ‘Condorcet winner’ is one that beats every other. There need not be a Condorcet winner, however, as illustrated by the possibility of cycles (a>b, b>c and c>a). In this case, the obvious generalisation is to go with the option that beats more others than any other[2].

It is worth noting at this stage that Condorcet’s procedure needn’t produce the most likely right answer, in spite of his well-known work on juries and probability. Suppose we have the following scenario:

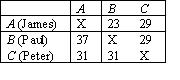
The number of votes for each option is in the appropriate row, with the columns indicating who they are paired against – thus we see B beats A 37 to 23. Note that in this case, C is a Condorcet winner, (narrowly) beating each of the other options 31 to 29.

If v (verité, the probability of an individual’s judgement being correct) is not much more than 0.5 then “the Borda rule is more likely to select the correct winner than is a search for the Condorcet winner, because Paul’s total score counts for more than Peter’s precarious and unreliable majority over him”[3]; i.e, because v is low and so is the winning majority, we cannot be very confident that C (Peter) really is better than B (Paul), or for that matter A (James). The 37 to 23 majority B (Paul) has over A (James), however, means – even with low v – we can be confident that B (Paul) is better than A (James). Whether he fully appreciated that his own logic should drive him to this result, Condorcet was firmly and explicitly against it – perhaps simply due to his personal hostility against Borda. Condorcet insisted we should eliminate A (James) for losing both comparisons, and that it would then be perverse to choose B (Paul) over C (Peter) when a majority prefer C (Peter). Against any alternative (Borda-inspired) method he wrote “The points method confuses votes comparing Peter and Paul with those comparing either Peter or Paul to James. As long as it relies on irrelevant factors to form its judgments, it is bound to lead to error”[4]. The last sentence makes somewhat explicit the principle to which he is appealing, independence of irrelevant alternatives – i.e. the choice between A and B should depend only on the relative merits of those two, not on C[5].

The inspiration behind both methods is to consider more than just first preferences, by looking at how voters rank other options. Thus they go some way towards reducing problems of intense minorities or majority tyranny, by producing a compromise that aims to be somewhat acceptable to all. We can remind ourselves what is at stake by re-producing the following table[6] (from last week), where both rules differ from each other and other common procedures (e.g. plurality, AV).

I (18 people): A D E _ C B
II (12): B E D _ C A
III (10): C B E D _ A
IV (9): D C E _ B A
V (4): E B D _ C A
VI (2): E C D _ B A

Six procedures give different results (I’ve highlighted the two most relevant to us):
1. Simple plurality: A
A wins, with 18 votes (options B-E scoring 12, 10, 9 and 6 respectively).
2. Plurality runoff (AV): B
B beats A in the second round, 37 votes (12+10+9+4+2) to 18.
3. Sequential runoff (STV): C
E, D, and B are eliminated. C wins the final vote, 37 to A’s 18.
4. Borda count: D
As above, each gets four points per first-preference, three points per second-preference… to zero points for a fifth (last) preference. D wins with 136 points = (18x3)+(12x2)+(10x1)+(9x4)+(4x2)+(2x2). A gets 72, B 101, C 107 and E 134.
5. Condorcet: E
The ‘Condorcet winner’ beats each of the other four options in pairwise comparison. Here E wins. E beats A 37-to-18, B 33-to-22, C 36-to-19, and D 28-to-27.
6. Approval voting: D and E tie
Everyone casts a vote for each option they consider ‘acceptable’ – here above the empty cell. A is approved by 18, B by 26, C by 21, and D and E by all 55. Thus D and E tie.

The Borda criterion attempts to most please everyone (collectively), rather than fully-pleasing most (as a simple plurality/majority system). Respecting everyone’s preferences would seem to promote utilitarian outcomes. It would elect someone who was widely popular, even if second choice, over someone who had a narrow majority of first preferences but was otherwise widely detested. For example:

51%: A, B, C,... Y, Z
49%: B, C, ... Y, Z, A

51% (i.e. a narrow majority) rank option A top and the other 25 in order, B-Z. The other 49% rank A as the worst (26th) option, but otherwise B-Z in order, 1st-25th. Here majority rule chooses A, which gets 51% of the vote to B’s 49%. A does not, however, maximise the total amount of good, because although 51% of people get their most-preferred option, the other 49% get their least-preferred[7]. Surely B would be better – first choice of 49% and second choice of the rest. This is the case in favour of the Borda count. The Borda count takes second-, third-, etc-preferences into account, as a proxy for intensity.

The problem with this method (assuming it’s trying to maximise utility, as described) is that it uses an ordinal ranking as proxy for intensity, when what’s really needed is some cardinal measure, that reflects the fact that, for a given voter, there may be a larger gap between A and B than B and C. We can see the problem with another example. Suppose an election consists of one conservative (right-wing), a communist (extreme left) and an extreme socialist (not quite as far left as the communist)[8]. Here, there’s very little difference between the communist and extreme socialist – many of those who vote for either might be almost indifferent between the two. Simply representing the voter’s rankings as (2, 1, 0) doesn’t reflect how much he prefers one to another, when on a cardinal scale it might be (100, 5, 4) if he was a conservative, or (10, 9, 1) if left-wing.

The Condorcet problem faces a similar problem. Pairwise comparison may find the extreme socialist wins over both the communist and the conservative. Nonetheless, while the extreme socialist may be the closest candidate to the median voter, he may be considerably to the left of that voter’s ideal. That is, he may simply be the ‘best of a bad bunch’. Similarly all the conservative-voters will presumably choose the socialist over the communist (unless being strategic), but that doesn’t mean they really endorse him[9]. It’s likely there will be a considerable range between the conservative and communist in which one could win the election either side of the median voter’s ideal. In a perfectly competitive (electoral) market, one might expect parties to converge on the median voter, but this needn’t happen if they have no more information than the votes, which simply won’t reveal that the median voter’s ideal is for (say) a left-of-centre administration, only that he voted for an extreme socialist.

The example is more problematic for the Borda count, however, because it raises another – perhaps the most fundamental – problem with it, the fact that its results depend on the number and range of options. Suppose, for example, a number of ‘blanks’ were added, to allow voters to more accurately represent their cardinal preferences[10]. These blanks would change the scores, and possibly the outcome. The same would happen if another genuine candidate, on either side, were to stand – e.g. another on the far right would (presumably) favour the conservative.

I don’t have a problem with the fact that Borda count fails independence of irrelevant alternatives per se, but I do think it’s problematic both that it still fails to reflect cardinal comparison and that because its result depends on the number and range of options it is manipulable. Candidates on one side of the spectrum are generally advantaged by more others standing on their side. The logical result would be everyone standing. If nothing else, it makes a complete ranking almost impossible for individual voters.

The Condorcet system isn’t as vulnerable in this respect. Admittedly it can fail to represent whether a candidate is really approved of, or just the best of a bad bunch (as in the above example). Condorcetians, however, might welcome extra candidates. E.g. suppose a left of centre candidate was to stand in the above case. It’s not guaranteed that he’d be a Borda winner, but very likely he’d be a Condorcet winner. The other major problem with the Condorcet method is that there need not be a Condorcet winner. This may be resolved by using the Copeland rule, as above.

Both methods have an understandable rationale in trying to count all of a voter’s preferences, and thus find a candidate acceptable to all. Neither, I think, fully succeeds, and both make a high demand on voters (expecting them to completely rank or compare candidates). I think the best method to use will depend on the context[11]. If the system is ‘open’ to new candidates/options coming forward, then the Condorcet (or Copeland) criterion will probably fare better, as it will avoid easy manipulation. On the other hand, once options are fixed, the Borda count may be better as it is likely to better reflect cardinal utilities than simple pairwise comparison.


[1] Quoted McLean and Urken (1987) Classics of Social Choice p.18
[2] The Copeland score is a measure of how many majorities each wins. Note in the previous example, each option has a Copeland score of one, so this still isn’t decisive. If there are more options, however, we may get a>b and a>c but a
[3] McLean and Urken (1987) p.34.
[4] Quoted McLean and Urken (1987) p.34.
[5] Consider a choice between cheese or tuna salad in a restaurant. If someone chose cheese, but changed their mind to tuna on being told chicken was also available, we’d certainly think it odd…
[6] Shepsle & Bonchek (1997) Analyzing Politics: Rationality, behavior and institutions pp.167-72.
[7] In a vote between A and B, this represents the case where an almost indifferent majority (the 51% that barely prefer A to B) out-vote what is presumably an intense minority.
[8] I assume a simple left-right economic dimension and single-peaked preferences.
[9] In this case, approval voting would seem attractive – presumably those on the right will only endorse the conservative, while many on the left will endorse both communist and socialist.
[10] E.g. ‘conservative, blank, blank, blank, socialist, communist’ or ‘socialist, blank, communist, blank, blank, conservative’.
[11] It could be said this is a principal lesson of social choice theory – that electoral/voting systems are not fixed, but tools, for us to use when and as appropriate for what we want.